Z grafami można spotkać się nad wyraz często. Takie najprostsze to struktura katalogów na dysku czy hierarchia przełożony-podwładny w firmie.
Bardziej skomplikowane znajdziesz w serwisach społecznościowych – np. drzewa znajomości. W sieciach teleinformatycznych będą to struktury połączeń pomiędzy węzłami. W nawigacji GPS – najkrótsze ścieżki od punktu A-Z itd.
Z punktu widzenia baz danych i tworzenia zapytań do tego typu struktur – zadania z grafami nie są trywialne. Szczególnie, gdy chcemy je rozwiązać za pomocą pojedynczej kwerendy.
W artykule tym, zaprezentuję kilka praktycznych scenariuszy wraz z rozwiązaniami bazującymi na SQL Server 2012. Mam nadzieję, że jeśli szukasz gotowych rozwiązań – uda Ci się zaadoptować prezentowane tutaj przykłady do swoich zastosowań.
W każdym z nich, wyzwaniem było napisanie rozwiązania w postaci pojedynczej kwerendy. Podejście proceduralne jest prostsze w zrozumieniu i może prowadzić do bardziej efektywnych rozwiązań (materializowanie pośrednie, indeksy na tabelach tymczasowych).
Trochę teorii
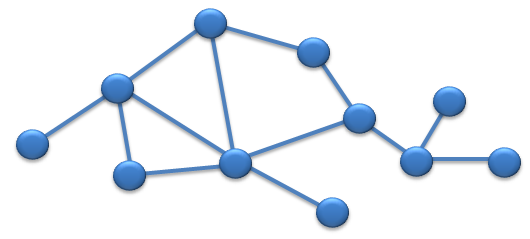
Patrząc na matematyczną teorię grafów, możemy mieć do czynienia z różnymi typami tych struktur. Na początek zajmiemy się grafami prostymi, wprowadzając przy okazji kilka podstawowych pojęć. Zbudujemy sobie tło do bardziej zaawansowanych scenariuszy.
Graf prosty (acykliczny, nieskierowany)
Graf prosty – to drzewo bez cykli, krawędzie nie są skierowane (nie ma ograniczeń kierunkowych) a pomiędzy każdą parą dowolnych wierzchołków, jest tylko jedna ścieżka. Dodanie jakiejkolwiek nowej krawędzi, spowoduje powstanie cyklu a usunięcie istniejącej doprowadzi do niespójności (podział grafu).
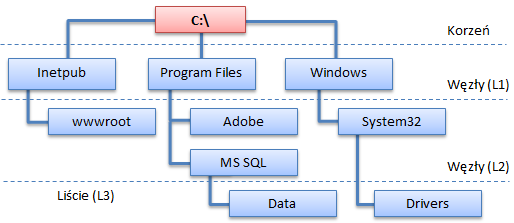
W przypadku, gdy jeden z wierzchołków, jest wyszczególniony (korzeń), mówimy o drzewie ukorzenionym. Grafy proste, ukorzenione są łatwe w implementacji w relacyjnych bazach. Tworzenie zapytań do takich struktur nie stwarza większych problemów. Tego typu graf, to na przykład organizacja systemu plikowego lub hierarchia pracownicza – przełożony/podwładny.
W typowej organizacji plików i katalogów zakładamy, że dany obiekt (plik lub katalog) nie może być w dwóch różnych miejscach jednocześnie (pomijając skróty, które mogą tworzyć cykle – o tym później). Do każdego węzła, jest tylko jedna ścieżka, prowadząca ,od korzenia grafu. Patrząc na tą strukturę, całość stanowi jedno spójne drzewo – graf prosty, ukorzeniony.
Podobnie w strukturze zatrudnienia. Dany pracownik zazwyczaj nie może mieć na tym samym poziomie dwóch bezpośrednich szefów. Droga eskalacji od podwładnego do przełożonego najwyższego szczebla, jest jedna.
Implementacja takiej struktury w bazie danych może być bardzo prosta. Realizuje się ją zazwyczaj, jako SELF JOIN, czyli złączenie tabeli samej ze sobą.
USE tempdb
GO
CREATE TABLE dbo.Folders (
ID INT NOT NULL PRIMARY KEY IDENTITY(1, 1),
Folder VARCHAR(100) NOT NULL,
Parent INT NULL REFERENCES dbo.Folders( ID )
);
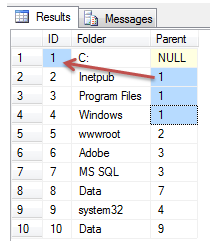
INSERT INTO dbo.Folders ( Folder ) VALUES ('C:');
INSERT INTO dbo.Folders ( Folder, Parent )
VALUES ('Inetpub',1),('Program Files',1),('Windows',1),('wwwroot',2),
('Adobe',3),('MS SQL',3),('Data',7),('system32',4),('Data',9);
select * from dbo.Folders
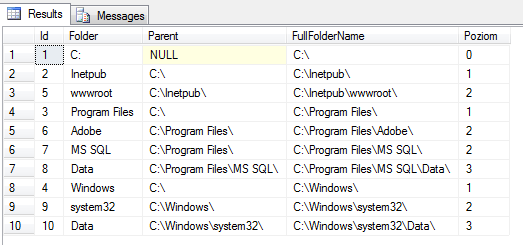
Zapytania SQL do takiego grafu, również nie są szczególnie skomplikowane. Wystarczy wykorzystać rekurencję wspólnych wyrażeń tablicowych (CTE Common Table Expressions) i przeszukiwać drzewo w głąb od korzenia do liści.
WITH Paths AS
(
SELECT Id, Folder, CAST(null AS VARCHAR(8000)) AS Parent,
CAST(Folder + '\' AS VARCHAR(8000)) FullFolderName, 0 as Poziom
FROM dbo.Folders
WHERE Parent IS NULL
UNION ALL
SELECT f.Id, f.Folder, p.FullFolderName,
CAST(ISNULL(p.Parent, '') + p.Folder + '\'
+ f.Folder + '\' AS VARCHAR(8000)) , p.Poziom +1
FROM dbo.Folders f INNER JOIN Paths p
ON f.Parent= p.ID
)
SELECT * FROM Paths
Order by FullFolderName
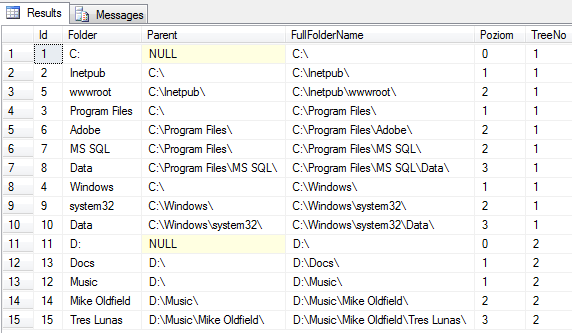
Takie podejście, załatwia również sprawę, w sytuacji, gdy mamy do czynienia ze zbiorem grafów prostych (las drzew). Zakotwiczenie CTE, identyfikuje wszystkie grafy i rekurencyjnie rozpina ja analogicznie jak poprzednio. Drzewa możemy ponumerować, do późniejszej analizy.
-- dorzućmy nowe drzewo - dysk D:
Insert into dbo.Folders(Folder) Values('D:');
Insert into dbo.Folders ( [Folder], [Parent] )
VALUES('Music',11),('Docs',11),('Mike Oldfield',12),('Tres Lunas',14);
WITH Paths AS
(
SELECT Id, Folder, CAST(null AS VARCHAR(8000)) AS Parent,
CAST(Folder + '\' AS VARCHAR(8000)) FullFolderName, 0 as Poziom,
ROW_NUMBER() OVER(ORDER BY FOLDER) as TreeNo
FROM dbo.Folders
WHERE Parent IS NULL
UNION ALL
SELECT f.Id, f.Folder, p.FullFolderName,
CAST(ISNULL(p.Parent, '') + p.Folder + '\'
+ f.Folder + '\' AS VARCHAR(8000)) , p.Poziom +1, TreeNo
FROM dbo.Folders f INNER JOIN Paths p
ON f.Parent= p.ID
)
SELECT * FROM Paths
Order by FullFolderName
W SQL Server od wersji 2008, mamy dostępny specjalny typ danych HierarchyId. Pozwala on na tworzenie bardziej zaawansowanych struktur w porównaniu do SELF JOINów. Za jego pomocą, można bardzo łatwo zamodelować scenariusz w którym istotna jest kolejność węzłów na danym poziomie hierarchii.
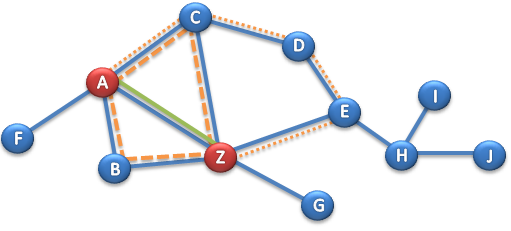
Graf nieskierowany z cyklami
Sytuacja staje się bardziej złożona, gdy mamy do czynienia z grafami, które posiadają cykle. Jest to typowy przykład architektury sieci teleinformatycznej, w której istnieją redundantne ścieżki w celu zapewnienia protekcji. Innym przykładem z którego korzystasz na co dzień to po prostu siatka połączeń drogowych pomiędzy miastami.
Wyszukiwanie ścieżek pomiędzy dowolnymi węzłami takiego grafu, musi uwzględniać możliwość zapętlenia. Dla każdej pary węzłów, może pojawić się wiele ścieżek. Zależnie od stopnia złożoności grafu (liczby węzłów i krawędzi) analiza możliwych dróg, może stanowić nie lada wyzwanie.
Skrypt z danymi do przeprowadzenia dalszych ćwiczeń od pobrania tutaj.
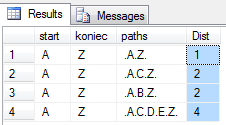
Implementacja takiego grafu w relacyjnej bazie danych, może być oparta o dwie tabele – węzłów i krawędzi między nimi. Na początek znajdźmy wszystkie ścieżki z punktu A-Z.
WITH Edges AS (
-- graf nieskierowany więc bierzemy pod uwagę krawędzi dwukierunkowo
-- A-Z i Z-A
SELECT Node1 as Start, Node2 as Koniec, Metric from EDGE
UNION
SELECT Node2, Node1 , Metric from EDGE
),
Paths as
(
-- rekurencyjne CTE
SELECT start , koniec ,
CAST('.' + start + '.' + koniec + '.' as varchar(max)) as paths, 1 as Dist
FROM Edges
UNION ALL
SELECT f.start, t.koniec , CAST(f.paths + t.koniec + '.' as varchar(max)),
F.dist+1
FROM Paths as F join Edges T on
-- wykluczenie cykli, czyli nie przechodzimy
-- przez żaden wierzchołek dwukrotnie
case when F.paths like '%.' + T.koniec + '.%' then 1 else 0 end = 0
and f.koniec = T.start
)
SELECT *
FROM Paths
WHERE Start = 'A' and Koniec = 'Z'
ORDER BY Dist
Powyższe podejście, pomimo że w jednej kwerendzie, jest słabe wydajnościowo i przy dużej liczbie (tysiące) węzłów / krawędzi działa po prostu bardzo wolno. Wystarczy spojrzeć na plan wykonania – przypomina zapytanie prawdziwie skorelowane. Alternatywnym rozwiązaniem jest podejście proceduralne, w którym tworzymy drzewa rozpinające.
Graf skierowany z cyklami i metrykami krawędzi
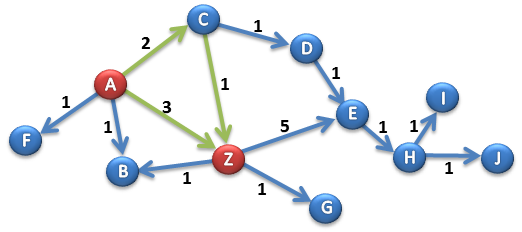
Wyszukiwanie najkrótszej drogi z punktu A-Z, zazwyczaj wymaga analizy jakości poszczególnych odcinków. Sytuacja taka ma zastosowanie zarówno w sieciach drogowych (autostrady, drogi lokalne), jak również informatycznych. W tych drugich, brane są pod uwagę zazwyczaj parametry jakościowe, czyli pasmo, opóźnienia, jitter. O ile w sieciach teleinformatycznych kierunkowość zazwyczaj jest tematem pomijalnym, o tyle drogi jednokierunkowe, to norma.
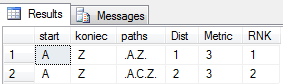
Bazując na danych z poprzedniego przykładu, wyznaczmy raz jeszcze najlepszą ścieżkę z A-Z, biorąc pod uwagę kierunkowość krawędzi oraz metryki. Nasz graf będzie wyglądał teraz tak :
W tej sytuacji widać, że pomiędzy węzłami A i Z powinny zostać znalezione tylko dwie ścieżki. Ponadto nie istnieje żadna ścieżka powrotna (Z > A). Zmodyfikujemy odrobinę zapytanie z poprzedniego przykładu :
WITH Edges AS (
-- graf skierowany więc bierzemy drogi takie jakie są
SELECT Node1 as Start, Node2 as Koniec, Metric from EDGE
),
Paths as
(
SELECT start , koniec ,
CAST('.' + start + '.' + koniec + '.' as varchar(max)) as paths, 1 as Dist, Metric
FROM Edges
UNION ALL
select f.start, t.koniec , CAST(f.paths + t.koniec + '.' as varchar(max)),
F.dist+1, F.Metric + T.Metric
from Paths as F join Edges T on
case when F.paths like '%.' + T.koniec + '.%' then 1 else 0 end = 0
and f.koniec = T.start
),
PathRanking as (
select *,
DENSE_RANK() OVER(Partition BY Start, Koniec Order by Metric, Dist) as RNK
from Paths)
Select * from PathRanking
where start = 'A' and koniec = 'Z';
Obydwie kosztują tyle samo (suma metryk jest identyczna), ale droga bezpośrednia A>Z ma mniej skoków, stąd zostaje wybrana jako najlepsza.
Las drzew (grafów) nieskierowanych, nieukorzenionych
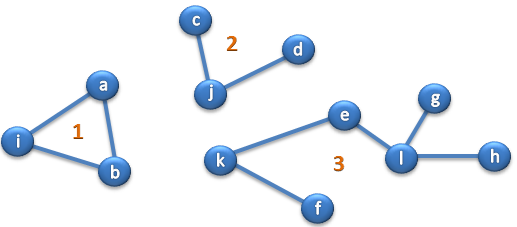
Bazując na powyższej metodzie, możemy pokusić się o rozwiązanie jeszcze jednego problemu. Zadaniem nietrywialnym, jest analiza zbioru grafów nieskierowanych bez korzenia. Tego typu struktury, spotkać możesz na przykład w serwisach społecznościowych.
Wyobraźmy sobie prostą tabelę powiązań (znajomości) pomiędzy użytkownikami. Pytanie w jaki sposób, określić czy dana osoba należy do jakiegoś kręgu (grupy znajomości mogą się tworzyć samoczynnie, bez dodatkowych relacji). Daną grupę, wyznaczają wszystkie osoby, które są w jakikolwiek sposób ze sobą powiązane (nawet pośrednio). Czyli tak naprawdę, musimy zidentyfikować przypisanie każdej krawędzi do określonego drzewa.
Rozwiązaniem w postaci jednej kwerendy, może być modyfikacja znanego już algorytmu wyznaczania ścieżek.
WITH Znajomi as
(
select * from (
VALUES ('a','b'),('a','i'),('b','i'),('c','j'),('d','j'),
('e','k'),('f','k'),('g','l'),('h','l'),('e','l')--,('a','e')
) as Tab(a,b)
),
Edge as (
select l.a as Start , cast( l.b as varchar) as Koniec, 1 as dist
from Znajomi l
union all
select cast( l.b as varchar) , l.a, 1
from Znajomi l
),
Paths as
(
select start , koniec , CAST('.' + cast(start as varchar(10))+ '.'
+ cast(koniec as varchar(10)) + '.' as varchar(max)) as path, dist
from Edge
UNION ALL
select f.start, t.koniec ,
CAST(f.path + cast(t.koniec as varchar(10)) + '.' as varchar(max)), F.dist+1
from Paths as F join Edge T on
case when F.path like '%.' + cast(T.koniec as varchar(10)) + '.%' then 1 else 0 end = 0
and f.koniec = T.start
)
,
Grupy as (
select c.a, c.b , SUBSTRING(max(path),2,CHARINDEX('.',max(path),2)-2) as GRID
from Znajomi c left join Paths r on r.Path like '%' + c.a + '.' +
cast( c.b as varchar) + '%' or r.Path like '%' + cast( c.b as varchar) + '.' + c.a + '%'
group by c.a, c.b
)
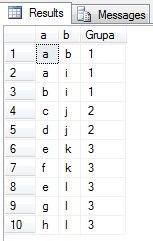
select a, b, DENSE_RANK() OVER(order by GRID) as Grupa from Grupy
Zauważ, że wykorzystałem tu pewne fundamentalne i oczywiste założenie. W danym drzewie, mamy możliwość dojścia do każdego węzła. W przeciwnym razie, dany graf byłby niespójny i stanowiłby tak naprawdę dwa lub więcej drzew.
W związku z tym, w ostatnim CTE (Grupy), grupuję po maksymalnej (równie dobrze mogłaby to by być minimalna) ścieżce, która zawiera identyfikatory węzłów. Na podstawie tego największego identyfikatora węzła, określam przynależność do grupy.
Podsumowanie
Zaprezentowane w tym artykule rozwiązania to tylko jedne z możliwych podejść. Proceduralnie można by je było rozwiązać znacznie prościej i szybciej. Jeśli masz propozycję rozwiązania tych zadań w bardziej efektywny sposób za pomocą jeden kwerendy – zapraszam do dyskusji !
Tematyka grafów jest znacznie szerzej (świetnie) opisana w książce Itzika Ben Gana „Inside Microsoft SQL Server 2008: T-SQL Querying” – polecam wszystkim.